Overview
This exercise will show you how to use GCD to build a spatially variable error model using fuzzy inference systems. Before we dive into the details of what an FIS is, how they work and how to build your own, we will simply treat an FIS as a black box that takes spatially variable inputs we can model and think relate to surface error, and it will spit out an FIS error surface. This is a powerful and flexible technique for modelling spatially variable error as illustrated below.
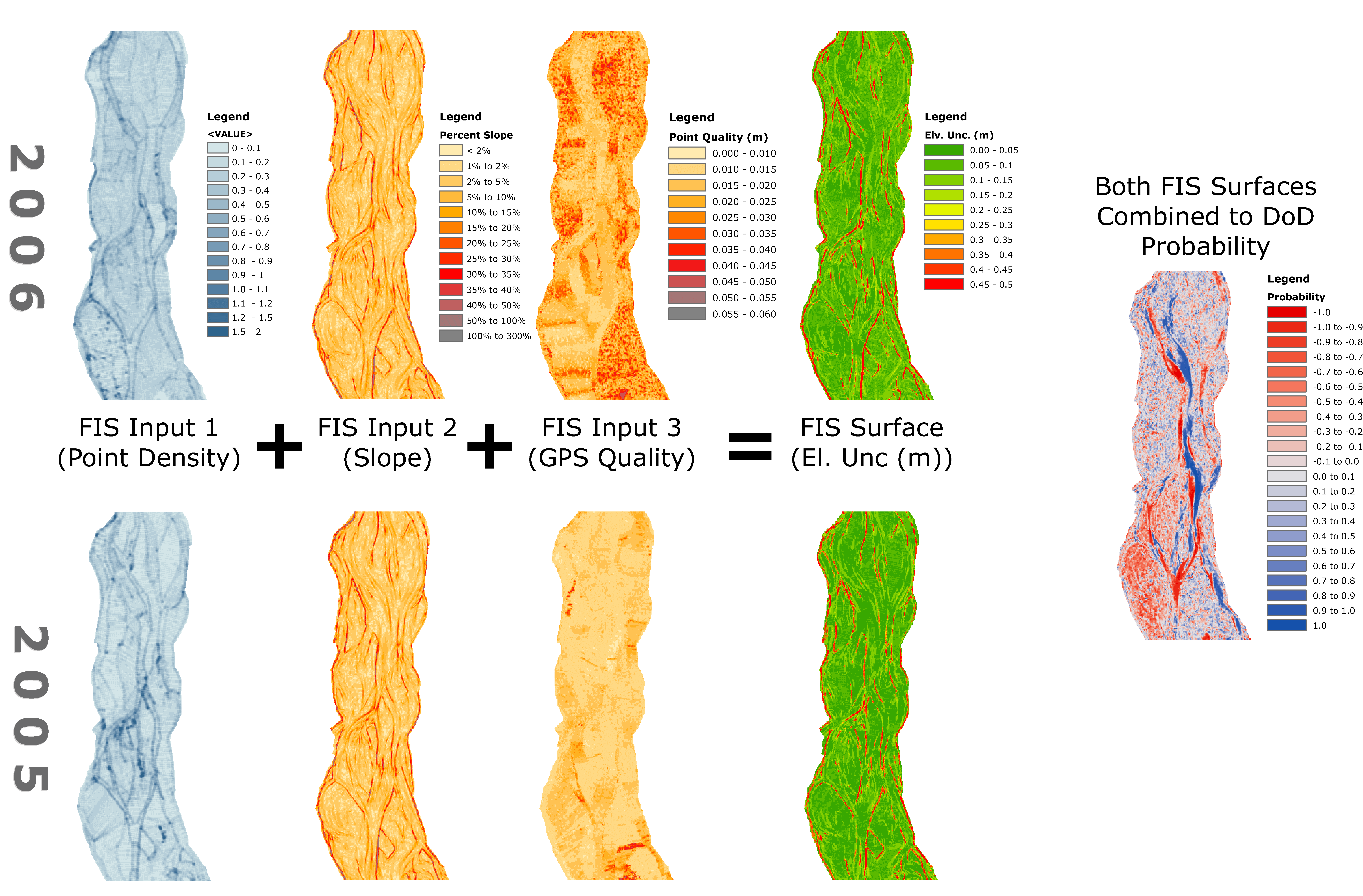
Figure illustrating independent estimate of spatially variable error for two surveys from Wheaton et al. (2010).
Data and Materials for Exercises
Datasets
- Feshie Example File of Data for this Exercise
- CHaMP Example (provided in class)
Data for 1 (above) is from Wheaton et al. (2010) & for 2 (above) is from Bangen et al. (2016)
-
- Bangen S‡ , Hensleigh J‡, McHugh P, and Wheaton JM. Error modeling of DEMs from topographic surveys of rivers using Fuzzy Inference Systems. Water Resources Research. DOI: 10.1002/2015WR018299.
- Wheaton JM, Brasington J, Darby SE and Sear D. 2010. Accounting for Uncertainty in DEMs from Repeat Topographic Surveys: Improved Sediment Budgets. Earth Surface Processes and Landforms. 35 (2): 136-156. DOI: 10.1002/esp.1886.
Prerequisite for this Exercise
- Some ArcGIS experience
- ArcGIS 10.X w/ Spatial Analyst Extension
- GCD Add-In
Step by Step
Exercise N - Part 1: RUNNING FIS ERROR MODELS
Suggested Path: C:\0_GCD\Exercises\N_FIS_Intro
- Start new ArcMap Document
- Create New GCD Project - Feshie in N
- Add survey DEM for 2006
- To start, as reminder, derive a spatially uniform error raster
- Load 2-input and 3-input FIS in FIS Library if not already present
- Derive point density and slope associated surfaces
- Run 2-Input point density, slope degrees FIS model to create new error surface
Exercise N - Part 2: RUNNING FIS ERROR MODELS
Suggested Path: C:\0_GCD\Exercises\N_FIS_Intro
- In same ArcMap Document
- Add a new point quality associated surface, PQ_2006.tif
- Run FIS with 3-Input Model (point quality, point density, slope degrees)
- Investigate difference between 2-Input and 3-Input FIS Error Surfaces
- Perform Change Detection between 2006 DEM using its 3-Input FIS Error model and 2007 DEM using its spatially uniform error model
- Compare results with a Change Detection between same DEM when both are using a spatially uniform error model.
Related Online Help or Tutorials for this Topic
← Back to Previous Tutorial Ahead to Next Tutorial →